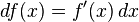unidad V

Tema: Aplicaciones de a derivada

subtema 5.1

Función creciente y decreciente

Función Creciente y Decreciente

ILUSTRACIÓN

Observa que parte de la gráfica se eleva, parte de la gráfica baja y parte de la gráfica es horizontal. En estos casos se dice que la gráficacrece, decrece o es constante.

Una función f se dice que es creciente si al considerar dos puntos de su gráfica, (x₁, f(x₁) ) y ( x₂, f(x₂) ) con

x₁	<	x₂	Se tiene que	f(x₁)	<	f(x₂).
Prevalece la relación <

Una función f se dice que es decreciente si al considerar dos puntos de su gráfica, (x₁, f(x₁) ) y ( x₂, f(x₂) ) con

x₁	<	x₂	Se tiene que	f(x₁)	>	f(x₂).
Cambia la relación de < a >

Una función f se dice que es constante si al considerar dos puntos de su gráfica, (x₁, f(x₁) ) y ( x₂, f(x₂) ) con

x₁	<	x₂	Se tiene que	f(x₁)	=	f(x₂).
Las y no cambian, son fijas

Considera la siguiente gráfica:

Los intervalos donde la gráfica es creciente son

[ 2.8, 3.6 ]

[ 5.2, 6 ]

El intervalo donde la gráfica es decreciente es

[ 3.6, 5.2 ]

El intervalo donde la gráfica es constante es

[ - 4, 2.8 ]

subtema 5.2

Extremos relativos y extremos absolutos

En matemáticas, los máximos y mínimos de una función, conocidos colectivamente como extremos de una función, son los valores más grandes (máximos) o más pequeños (mínimos), que toma una función en un punto situado ya sea dentro de una región en particular de la curva (extremo local) o en el dominio de la función en su totalidad (extremo global o absoluto).¹ ² ³ De manera más general, los máximos y mínimos de un conjunto (como se define en teoría de conjuntos) son los elementos mayor y menor en el conjunto, cuando existen. El localizar valores extremos es el objetivo básico de la optimización matemática.

subtema 5.3

Prueba de la primera derivada para la determinación de máximos y mínimos

subtema 5.4

Concavidad, puntos de inflexión y prueba de la segunda derivada

En los puntos de inflexión hay cambio de concavidad a convexidad o viceversa.

Cálculo de los puntos de inflexión

f(x) = x³ − 3x + 2

1. Hallamos la derivada segunda y calculamos sus raíces.

f''(x) = 6x 6x = 0 x = 0.

2. Realizamos la derivada tercera, y calculamos el signo que toman en ella los ceros de derivada segunda y si:

f'''(x) ≠ 0 Tenemos un punto de inflexión.

f'''(x) = 6 Será un punto de inflexión.

3. Calculamos la imagen (en la función) del punto de inflexión.

f(0) = (0)³ − 3(0) + 2 = 2

Punto de inflexión: (0, 2)

Cálculo de los puntos de inflexión conociendo los intervalos de concavidad y convexidad

Los puntos de inflexión son los puntos de la función en que ésta pasa de cóncava a convexa o vicecersa.

Ejercicios

Tenemos un punto de inflexión en x = 0, ya que la función pasa de concava a convexa.

Punto de inflexión (0, 0)

Dominio

subtema 5.5

Optimización de funciones económicos-administrativas: maximización de funciones de ingreso, utilidad y beneficios; minimización de funciones de costos y costos promedio.

subtema 5.6

Elasticidades: elasticidad de la demanda y elasticidad del ingreso

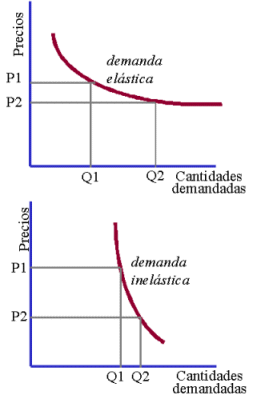
Hay algunos bienes cuya demanda es muy sensible al precio, pequeñas variaciones en su precio provocan grandes variaciones en la cantidad demandada. Se dice de ellos que tienen demanda elástica. Los bienes que, por el contrario, son poco sensibles al precio son los de demanda inelástica o rígida. En éstos pueden producirse grandes variaciones en los precios sin que los consumidores varíen las cantidades que demandan. El caso intermedio se llama de elasticidad unitaria.

La elasticidad de la demanda se mide calculando el porcentaje en que varía la cantidad demandada de un bien cuando su precio varía en un uno por ciento. Si el resultado de la operación es mayor que uno, la demanda de ese bien es elástica; si el resultado está entre cero y uno, su demanda es inelástica.

Los factores que influyen en que la demanda de un bien sea más o menos elástica son:

1) Tipo de necesidades que satisface el bien. Si el bien es de primera necesidad la demanda es inelástica, se adquiere sea cual sea el precio; en cambio si el bien es de lujo la demanda será elástica ya que si el precio aumenta un poco muchos consumidores podrán prescindir de él.

2) Existencia de bienes sustitutivos. Si existen buenos sustitutos la demanda del bien será muy elástica. Por ejemplo, un pequeño aumento en el precio del aceite de oliva puede provocar que un gran número de amas de casa se decida por usar el de girasol.

La elasticidad de la demanda. Pulse en la imagen para ver una explicación animada.

PULSE AQUÍ PARA VER OTRAS PRESENTACIONES MULTIMEDIA

3) Importancia del bien en términos de coste. Si el gasto en ese bien supone un porcentaje muy pequeño de la renta de los individuos, su demanda será inelástica. Por ejemplo, el lápiz. Las variaciones en su precio influyen muy poco en las decisiones de los consumidores que desean adquirirlos.

4) El paso del tiempo. Para casi todos los bienes, cuanto mayor sea el período de tiempo considerado mayor será la elasticidad de la demanda. Puede ser que al aumentar el precio de la gasolina, su consumo no varíe mucho, pero al pasar el tiempo podrá ser substituida en algunos de sus usos por el carbón, en otros usos por el alcohol, de forma que la disminución en la demanda sólo se nota cuando pasa el tiempo.

5) El precio. finalmente hay que tener en cuenta que la elasticidad de la demanda no es la misma a lo largo de toda la curva. Es posible que para precios altos la demanda sea menos elástica que cuando los precios son más bajos o al revés, dependiendo del producto de que se trate

*Hay algunos bienes cuya demanda es muy sensible al precio, pequeñas variaciones en su precio provocan grandes variaciones en la cantidad demandada. Se dice de ellos que tienen demanda elástica. Los bienes que, por el contrario, son poco sensibles al precio son los de demanda inelástica o rígida. En éstos pueden producirse grandes variaciones en los precios sin que los consumidores varíen las cantidades que demandan. El caso intermedio se llama de elasticidad unitaria.

unidad IV
Tema: complementarios de diferenciación

Si una ecuación define de manera implícita a y como función de x [en vez de definirla en forma explícita, en forma y = f (x )], entonces dy/dx puede encontrarse por diferenciación implícita. Con este método, tratamos a y como una función de x y diferenciamos ambos miembros de la ecuación con respecto a x. Al hacer esto recuerde que:

Por último, despejamos de la ecuación a dy / dx, Las fórmulas para derivar logaritmos naturales funciones exponenciales son:

Para diferenciar funciones logarítmicas y exponenciales con base diferente a e, primero la función puede transformarse a base e y luego diferenciarse el resultado. De manera alterna, pueden aplicarse las fórmulas de diferenciación

Suponga que f (x) consiste en productos, cocientes o potencias. Para diferenciar y = log[ f (x) ], puede ser conveniente usar las propiedades de los logaritmos para reescribir logh [f(x)] en términos de logaritmos más sencillos y luego diferenciar esa forma.

Para diferenciar y = f(x), donde f(x) consiste en productos, cocientes o potencias, puede utilizarse el método de diferenciación logarítmica. En este método, tomamos el logaritmo natural de ambos miembros de y = f(x) para obtener lny = ln [f (x) ].

Después de simplificar ln [f (x) ] por medio de las propiedades de los logaritmos, diferenciamos ambos miembros de ln y = ln[f(x)] con respecto a x y luego despejamosy'. La diferenciación logarítmica se utiliza también para diferenciar y = uv donde u y v son funciones de x.

Como la derivada f'(x) de una función y = f(x) es a su vez una función, podemos diferenciarla de manera sucesiva para obtener la segunda derivada f"(x), la tercera derivadaf'"(x) y otras derivadas de orden superior.

Subtema 4.1

Derivada de una funciones logarítmicas

subtema 4.2

Derivadas de funciones exponenciales

La derivada de la función exponencial ea igual a la misma función por el logaritmo neperiano de la base y por la derivada del exponente.

Derivada de la función exponencial de base e

La derivada de la función exponencial de base e ea igual a la misma función por la derivada del exponente.

Ejemplos

subtema 4.3

Diferenciación implícita

v Se dice que una función está definida explícitamente cuando se da de la forma y = f (x); esto es cuando se da y despejada en términos de x. En cambio, si en una ecuación, como por ejemplo, 2yx = cos3y, existe una función tal que y = f (x), se dice que y es una función que está definida implícitamente por la ecuación. Una ecuación en x e y puede definir a más de una función implícita.v En muchas ocasiones no se puede resolver explícitamente una función dada en forma implícita. v Es posible hallar la derivada de una función expresada implícitamente, sin necesidad de transformarla en su equivalente explícita.

S o l u c i o n e s

subtema 4.4

Diferenciación logarítmica

subtema 4.5

Derivadas de orden superior

es una función diferenciable, es posible considerar su función derivada como:
$f'=\{(x,y)/\;y=D_{x}f(x)\}$ para

en el dominio

.
Si para algunos valores $x \in M$ existe el $\displaystyle{\lim_{h \rightarrow{0}}{\frac{f'(x+h)-f'(x)}{h}}}$ se dice que existe la segunda derivada de la función

que se denota por

o $D_{x}^{2}f(x)$ , que equivale a $D_{x}[D_{x}f(x)]$ . O sea, la segunda derivada de la función

se obtiene derivando la primera derivada de la función.
Ejemplos:

Si $f(x)=5x^{3}+6x^{2}-5x+1$ entonces:
$f'(x)=15x^{2}+12x-5$ y
Si $\displaystyle{g(x)=\frac{x^{2}+3x}{x-1}}$ entonces:
$\displaystyle{g'(x)=\frac{(x-1)(2x+3)-(x^{2}+3x)}{(x-1)^{2}}=\frac{x^{2}-2x-3}{(x-1)^{2}}}$ y derivando nuevamente
$\displaystyle{g''(x)=\frac{(x-1)^{2}(2x-2)-(x^2-2x-3)2(x-1)}{(x-1)^{4}}}$
$=\displaystyle{\frac{(x-1)^{2}(2x-2)-(x^{2}-2x-3)2(x-1)}{(x-1)^{4}}}$
$=\displaystyle{\frac{(x-1)[(x-1)(2x-2)-(x^{2}-2x-3)]}{(x-1)^{4}}}$
Por tanto $\displaystyle{g''(x)=\frac{8}{(x-1)^{3}}}$

Similarmente podemos decir que la derivada de $D_{x}^{2}f(x)$ respecto a "x" es la tercera derivada de

respecto a "x" que se denota $D_{x}^{3}f(x)$ o

.
La derivada de la tercera derivada es la cuarta derivada $D_{x}^{4}f(x)$ y así podríamos continuar sucesivamente hasta la enésima derivada de

que se denota por $D_{x}^{n}f(x)$ o $f^{(n)}(x)$ . Generalmente se habla del orden de la derivada; así la primera derivada es la derivada de primer orden, la segunda es la de segundo orden, la enésima derivada es la derivada de orden n.
Ejemplos:

Determinar $g''(x)\; \mbox{si}\; g(x)=\sqrt{x^{2}+2x+3}$ , donde $D_{g}=I\!\!R$
Solución:
Obtenemos primero
$\displaystyle{g'(x)=\frac{x+1}{\sqrt{x^{2}+2x+3}}}$
Luego:
$\displaystyle{g''(x)=\frac{\sqrt{x^{2}+2x+3}-(x+1)\cdot \frac{(x+1)}{\sqrt{x^{2}+2x+3}}}{\sqrt{(x^{2}+2x+3)^{2}}}}$ y se tiene que:
$\displaystyle{g''(x)=\frac{2}{(x^{2}+2x+3)\sqrt{x^{2}+2x+3}}}$
Determinar $\displaystyle{f'''(x)\;\mbox{si}\; f(x)=2x^{\frac{1}{3}}-4x^{\frac{2}{5}}+x}$
Solución:
Se tiene que:

Por último:
Si $y=\sqrt{x}$ determinar $D_{x}^{n}y$ .
En este caso debemos dar una forma general para la derivada de orden n, partiendo de las regularidades que se presentan en las primeras derivadas que calculemos.
Así:

.
.

subtema 4.6

Diferenciales

En matemáticas concretamente en cálculo diferencial, el diferencial es un objeto matemático que representa la parte principal del cambio en la linealización de una función y = ƒ(x) con respecto a cambios en la variable independiente. Existen diversas definiciones de diferencial en diversos contextos.

Informalmente, el diferencial dy se define en cursos introductorios mediante la expresión:

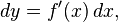
$dy = f'(x)\,dx,$

donde

f'(x)

es la derivada de f con respecto a x, y donde dx es una variable real adicional (de manera que dy es una función de dos variables x, y dx). La notación es tal que la expresión:

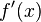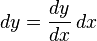
$dy = \frac{dy}{dx}\, dx$

donde la derivada es representada en la notación de Leibniz dy/dx, se mantiene, y es consistente con respecto a la derivada como el cociente de diferenciales.

El significado preciso de las variables dy y dx depende del contexto de aplicación y del nivel de rigor matemático requerido. Según consideraciones matemáticas rigurosas modernas, las notaciones dy y dx son simplemente variables reales y son manipuladas como tales. El dominio de estas variables puede tomar un significado geométrico particular si el diferencial es considerado como una forma diferencial, o significado analítico si el diferencial es considerado como una aproximación lineal al incremento de una función. En aplicaciones físicas, a menudo, se requiere que las variables dx y dy sean sumamente pequeñas (infinitesimales).

Definición[editar]

Para funciones de variables reales es posible definir el diferencial rigurosamente interpretándolo como una 1-forma. Así el diferencial está definido en los tratamientos modernos del cálculo diferencial de la siguiente manera.¹ El diferencial de una función ƒ(x) de variable real

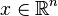x\in \R^n

es la función df: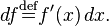

$df \stackrel{\rm{def}}{=} f'(x)\,dx.$

donde dx y df son covectores del espacio cotangente

T^*\R^n

que es isomorfo al propio

\R^n

. Uno, o los dos, argumentos pueden ser suprimidos: ej., se puede ver df(x) o simplemente df. Si y = ƒ(x), el diferencial también puede ser escrito dy. Dado que dx(x, Δx) = Δx es convencional escribir dx = Δx, de manera que la igualdad

df(x) = f'(x) \, dx

se mantiene.

subtema 4.7
Aplicaciones alas ciencias económico administrativas: costo marginal, ingreso marginal, utilidad marginal, propensión marginal y propensión margina al ahorro.

*La derivada es un concepto que tiene variadas aplicaciones. Se aplica en aquellos casos donde es necesario medir la rapidez con que se produce el cambio de una magnitud o situación.Por ejemplo, cuando se refiere a la gráfica de dos dimensiones de $f$ , se considera la derivada como la pendiente de la recta tangente del gráfico en el punto $x$ . Se puede aproximar la pendiente de esta tangente como el limite cuando la distancia entre los dos puntos que determinan una recta secante tiende a cero, es decir, se transforma la recta secante en una recta tangente. Con esta interpretación, pueden determinarse muchas propiedades geométricas de los gráficos de funciones.

Matematicas 1

sábado, 23 de mayo de 2015